Os logaritmos foram criados no século XVII com o objetivo de facilitar a resolução de funções exponenciais, quando os lados da igualdade não forem facilmente redutíveis a exponenciações de mesma base.
Veja:
$2^x$=$6$
No exemplo acima, para resolvermos esta equação, deveríamos transformar o número 6 em uma exponenciação, onde a base deveria ser 2. Assim, cortaríamos a base e igualaríamos os expoentes. Porém, transformar o 6 em uma exponenciação de base 2 é uma tarefa bastante difícil, pois o expoente não seria um número inteiro.
Foi com o objetivo de resolver mais facilmente estas equações que foi criado o logaritmo.
Definição
Um logaritmo é escrito da seguinte maneira:
$log_{a}{b}$=$x$
Onde:
a = base
b = logaritmando
x = logaritmo
Por extenso: logaritmo de b na base a é igual a x
Para calcular uma expressão do tipo, fazemos o seguinte:
Vejamos um exemplo numérico:
$log_{5}{25}$=$x$
$5^x$=$5^5$
$x=5$
Note que, ao aplicarmos a definição, obtemos uma equação exponencial. A partir daí, a resolução pode ser feita normalmente, igualando as bases e as eliminando em seguida.
Como condição de existência, b e a devem ser maior que 0, isto é, não podem ser um número negativo, e a tem que ser diferente de 1.
Exercício de fixação 1
Descubra o valor de x: $log_{\frac{1}{2}}{\sqrt{64}}=x$
Resolução:
$(\frac{1}{2})^x=\sqrt{64}$
$(\frac{1}{2})^x=8$
$(\frac{1}{2})^x=2^3$
$2^-x=2^3$
$x=-3$
Propriedades
A partir da definição, é possível depreender algumas propriedades, que serão importantes para a resolução de alguns exercícios.
São elas:
I. $log_{a}{a}$ =$1$, pois $a^1=a$
II. $log_{a}{1}$ =$0$, pois $a^0=1$
III. $log_{a}{a}^k$ =$k$, pois $a^k=a^k$
IV. $a^{log_{a}{b}}$ =$b$
A explicação para a última das propriedades é bastante simples.
Se $log_{a}{b}$=$log_{a}{b}$, então $a^{log_{a}{b}}$=$b$
Note que, se aplicarmos a definição à igualdade $log_{a}{b}$ = $log_{a}{b}$ (obtido através da lógica), obteremos exatamente a definição apresentada pela última propriedade.
Exercício de fixação 2
Se $log_{a}{(ab)}=10$, então $log_{a}{b}$ é igual a:
Resolução:
$log_{a}{(ab)}=10$
$log_{a}{a}+log_{a}{b}=10$ (Propriedade V, que será vista a seguir)
$1+log_{a}{b}=10$ (Propriedade I)
$log_{a}{b}=9$
Outras propriedades muito importantes e que devem ser decoradas para a resolução dos exercícios são:
V. $log_{a}(b.c)$ =$log_{a}b+log_{a}c$
VI. $log_{a}(\dfrac{b}{c})$ =$log_{a}b-log_{a}c$
VII. $log_{a}{b}^c$ =$c.log_{a}b$
VIII. $log_{a^c}{b}$ =$\dfrac{1}{c}.log_{a}b$
Exercício de fixação 3
(VUNESP) Se $x=log_{8}{25}$ e $y=log_{2}{5}$, então
a) $x=y$
b) $2x=y$
c) $3x=2y$
d) $x=2y$
e) $2x=3y$
Resolução:
$x=log_{8}{25}$
$x=log_{2^3}{5^2}$
$x=\frac{2}{3}log_{2}{5}$ (Propriedades VII e VIII)
$x=\frac{2}{3}y$
$3x=2y$
Resposta: C
Exercício de fixação 4
(FEI-SP) Se $log_{10}{2}=a$ e $log_{10}{3}=b$, escrevendo $log_{10}{\frac{32}{27}}$ em função de a e b, obtemos
a) $2a+b$
b) $2a-b$
c) $2ab$
d) $\frac{2a}{b}$
e) $5a-3b$
Resolução:
$log_{10}{\frac{32}{27}}$
$log_{10}{\frac{2^5}{3^3}}$
$log_{10}{2^5}-log_{10}{3^3}$ (Propriedade VI)
$5.log_{10}{2}-3.log_{10}{3}$
$5.a-3.b$ (Propriedade VII)
Resposta: E
Mudança de base
Em muitos casos, na resolução de exercícios, precisamos alterar a base de um dos logaritmos da equação, com o objetivo de poder utilizar as outras propriedades descritas acima e, assim, obter o resultado final. Esta mudança ocorre através da seguinte propriedade:
$log_{a}b$ =$\dfrac{log_{c}b}{log_{c}a}$
Vamos a um exemplo:
Escreva $log_{3}5$ na base 5:
$log_{3}5$ =$\dfrac{log_{5}5}{log_{5}3}$=$\dfrac{1}{log_{5}3}$
Equações logarítmicas
Por vezes, é comum encontrarmos a incógnita não no logaritmo, mas na base ou no logaritmando. É o que chamados de equações logarítmicas. Para resolver este tipo de exercício, devemos usar, além das propriedades, as condições de existência. Vejamos sua aplicação no exercício abaixo.
Exercício de fixação 5
Resolver, em $\mathbb{R}$, a equação $log_{2}{(1-5x)}=-3$
Resolução:
Primeiramente, devemos aplicar a condição de existência, com o objetivo de excluir os valores de x que a violem. Para isso, devemos lembrar que o logaritmando deve ser maior que zero. Assim:
$b>0$
$1-5x>0$
$-5x>-1$
$5x<1$ (ao multiplicarmos ambos os lados por -1, o sinal de menor se inverte)
$x<\frac{1}{5}$
Assim, x deve ser menor que $\frac{1}{5}$ para que b seja maior que 0
Agora, devemos aplicar as propriedades.
$2^{-3}=1-5x$
$\frac({1}{2})^3=1-5x$
$\frac{1}{8}=1-5x$
$1=8-40x$
$40x=7$
$x=\frac{7}{40}$
Como $\frac{7}{40} < \frac {1}{5}$, podemos concluir que $S=\frac{7}{40}$

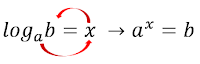

EmoticonEmoticon