Gráfico velocidade x tempo
No MU, o gráfico de velocidade x tempo é sempre uma linha horizontal reta, visto que a velocidade não se altera em função do tempo. Basicamente, teremos dois tipos de gráfico no MU, dependendo da característica do movimento. Para explicar estas características, vamos retomar o enunciado do exercício exemplo da postagem anterior:
Felipe mora em Florianópolis/SC. Ágata, em Tubarão/SC. Ambos partem, ao mesmo tempo, de suas cidades, com o objetivo de se encontraram. Felipe dirige em velocidade constante de 100km/h, enquanto Ágata dirige com aceleração nula e com velocidade de 120km/h. As cidades são separadas por 110km [...] Vamos considerar Florianópolis na posição 0km (origem do sistema de referência).Para o entendimento completo deste artigo, recomendamos a leitura de "Movimento uniforme (MU) e movimento retilíneo e uniforme (MRU)".
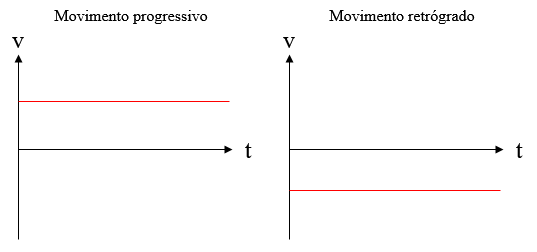
Movimento progressivo - Um movimento é progressivo quando o corpo se movimenta de uma posição convencionada como menor para outra convencionada como maior. No exercício anterior, por exemplo, Felipe fazia um movimento progressivo, pois partia do km 0 (Florianópolis) e ia para o km 110 (Tubarão). Por consequência, a velocidade é positiva.
Movimento retrógrado - Um movimento é retrógrado quando o corpo se movimenta de uma posição convencionada como maior para outra convencionada como menor. No exercício anterior, Ágata fazia um movimento retrógrado, visto que ela partia do km 110 (Tubarão) em direção ao km 0 (Florianópolis). Por isso sua velocidade era negativa.
Assim, a horizontal que representa o valor da velocidade estará em cima do eixo das abcissas (x) quando o movimento for progressivo, e abaixo dela quando o movimento for negativo.
Outra propriedade importante deste gráfico é a área. Calculando a área entre a linha que representa a velocidade e o eixo x, obteremos o espaço percorrido.
Gráfico posição x tempo
O gráfico de posição x tempo será como um gráfico de uma função de primeiro grau. Se analisarmos a função horária, que relaciona justamente as variáveis posição e tempo, veremos que se trata de um equação do tipo, Veja:
$S_f=S_i+v.t_f$
$y=b+a.x$
Assim, o gráfico posição x tempo será igual a um gráfico de uma função de primeiro grau, ou seja, uma reta inclinada.
Bem como no exemplo anterior, o gráfico vai variar dependendo do fato do movimento ser progressivo ou retrógrado. Quando a linha for ascendente, teremos um movimento progressivo (as posições aumentam conforme o tempo passa). Quando a linha for descendente, teremos um movimento retrógrado (as posições diminuem conforme o tempo passa).
Nestes gráficos, uma propriedade fundamental é a da inclinação. Se voltarmos à comparação feita entre a função horária e a função do primeiro grau, veremos que a velocidade é o equivalente ao $a$, o que, na matemática, representa o coeficiente angular. Isto quer dizer que, quanto mais inclinada for a reta, maior a velocidade. Da mesma forma que, se a inclinação for negativa, a velocidade também será.
Exercício de fixação 1
(Mackenzie-SP) Correndo com uma bicicleta, ao longo de um trecho retilíneo de uma ciclovia, uma criança mantém a velocidade constante de módulo igual a 2,50 m/s. O diagrama horário da posição para esse movimento está ilustrado na figura.
Segundo o referencial adotado, no instante t = 15,00 s, a posição x da criança é igual a
a) –37,50 m.
b) –12,50 m.
c) 12,50 m.
d) 37,50 m.
e) 62,50 m.
Resolução:
Primeiramente, tiramos os dados do enunciado:
$v=-2,5m/s$ (gráfico decrescente)
$t=15s$
$x=?$
Se formos montar a função horária com estes dados, vamos ter:
$S_f=S_i-2,5.15$
Observe que, para obter $S_f$, precisamos primeiramente de $S_i$. Podemos encontrar este valor através dos dados que temos no gráfico, montando sua função horária:
$25=S_i-2,5.30$
$S_i=75+25$
$S_i=100$
Sabendo que $S_i=100$, podemos resolver a equação anterior:
$S_f=100-2,5.15$
$S_f=62,5m$
Resposta: E





EmoticonEmoticon